This selection of coin Puzzles was first submitted by ThinkFun, now part of Ravensburger, as part of their Puzzle Playground. As the original website no longer exists we have been granted authorization and kept their instructions and credits, images and text are from their old webpage.
If you have any other puzzles you would like to see included here please let us know via support@g4gfoundation.org
- You’ll Need: coins, or pen/pencil

Keep It Even
by Boris Kordemsky
Sixteen coins fill the 4 x 4 grid as shown. Remove six of them so that each row and column contains an even number of coins.

Nob’s H-2-O
by Nob Yoshigahara
The title of the puzzle describes it quite well. The additional information is that the letters are made of coins and there is a limit on the moves. Go right to the rules to find out more!
Eight identical coins are arranged in the H letter shown in the upper left corner.Can you convert the H letter into the O letter shown in the lower right corner observing one simple rule: move one coin at a time so that in its new position it touches at least two other coins from the unmoved group, except the case when this coin (marked as @) makes a straight line triad, like O@O.

Coin Exchange
by Peter Grabarchuk
Invert a capital L of coins into another L only by sliding of the coin pairs. Now that you know this simpLe ruLe, it couLdn’t be very difficuLt to sLide the coins up to the soLution…
Take six coins of the same size and arrange them in the capital L altering their heads and tails as shown in the illustration – left position.
The goal is to make another L with all the coins having their heads and tails exchanged as shown in the right position of the illustration. It should be performed in the fewest possible number of moves.
A move consists of sliding a pair of the two adjoining coins to a new place. You have to slide the coins only orthogonally; it means that you are not allowed to rotate the pair of coins while you move it. The final L not necessarily has to be formed exactly at the same spot as the start L was.
In Puzzleland
by Sam Loyd
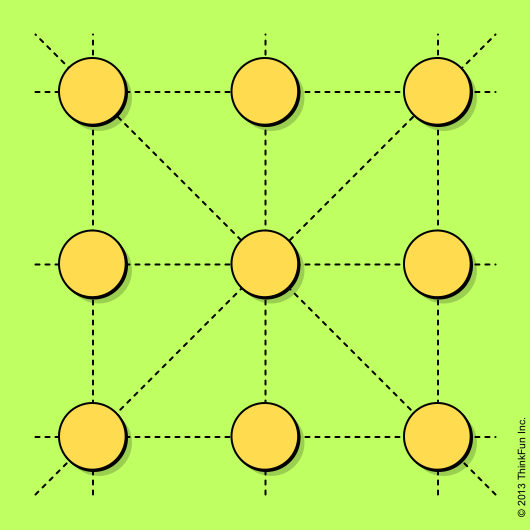
Nine coins. Placed in a square they form eight rows of three coins each. Theory states they can form more rows of three coins. How to get it in practice?
A square of nine coins shown in the illustration contains eight rows of three coins each (indicated with the lines) – three horizontal rows, three vertical rows and two main diagonals.
The object is to move the minimum possible number of coins to new positions so that to form ten rows of three coins each.
Coin Squad
by Serhiy Grabarchuk, Jr.
Form a little coin squad, and change then its order by a simple slide the coins in pairs. It really doesn’t require the military tactics.
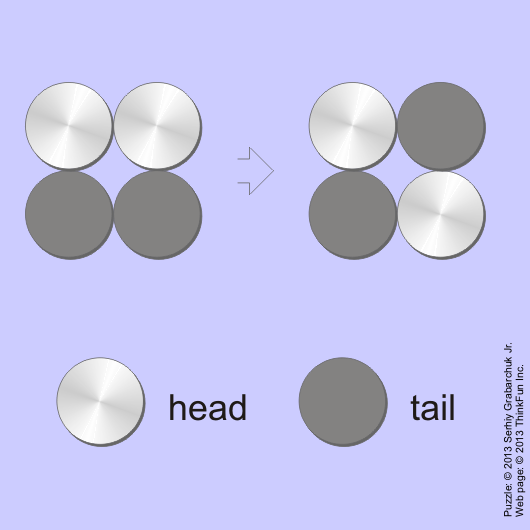
Take four coins of the same size and make a square as shown in the far left square in the illustration; two coins – heads up in the top row, and the other two – tails up in the bottom row.
The object is to make another square with two coins heads up on one diagonal and with two coins tails up on the other – as shown in the right square in the illustration.
This should be performed in the shortest possible number of moves.
A move consists of sliding a pair of the two adjoining coins to a new place. You have to slide the coins only orthogonally; it means that you are not allowed to rotate the pair of coins while you move it. The final square not necessarily needs to be formed exactly at the same spot as the start square was.

Coin Triangle
by Serhiy Grabarchuk
Change the triangle into a square by moving the minimum of the coins. How many coins will you need to move to do this?
Change the triangle into a square by moving the minimum of the coins.
How many coins will you need to move to do this?
Move the coins dragging them.

The Five Pennies
by Henry E. Dudeney
Maybe it is easy to place four coins in such a way that each coin touches every other one. But what would you say about five coins? Yes, it is possible too.
It is quite easy to place four pennies in such a way that each penny touches every other one. Just place three of them on the table in the form of a triangle so that they touch one another, and then lay the fourth penny on top of this triangle – as shown on the far left.
Now add one more penny and try to do the same thing with five pennies – again every penny has to touch every other penny.

Coin Cup
by Serhiy Grabarchuk, Jr.
You don’t have to win a playoff to get the cup turn over. Just win your own set in two coins and make the cup stand upside down.
Make the depicted cup with eight coins of the same size as shown in the illustration.
The object is to move only two of them in a new position to get the cup standing upside-down.
You’re allowed to move the coins as you wish but at the end the cup has to have exactly the same shape only rotated at 180 degrees from its start position.

The Six Pennies
by Henry E. Dudeney
Transform the two rows of coins into a perfect hexagon simply sliding them. And there is only one additional spec for the sliding…
Place six pennies on the table in two rows as shown at the top left. The object is to turn these two rows into the coin circle shown in the bottom right figure in only three moves.
A move consists of sliding one coin to a new position, where the moved coin has to touch two other coins.

Coins & Triangles
by Kobon Fujimura
Remove some coins from a big coin triangle containing ten coins and a lot of smaller equilateral triangles so that no equilateral coin triangles remain.
When the centers of any three coins lie in the corners of an equilateral triangle of some size, such coins form an equilateral coin triangle. How many equilateral coin triangles of different sizes can you count in the figure?
The object of the puzzle now is to remove the minimum number of coins so that no equilateral coin triangles remain. In other words, centers of any three coins among those that remained don’t lie in the corners of an equilateral triangle.
To remove a coin simply click it. Click on the coin again to restore it.

Collating the Coins
by Martin Gardner
Change the order of five coins in a chain from big-small-big-small-big to big-big-big-small-small. Another classic puzzle gem!
Arrange five coins (three bigger and two smaller ones) as shown above (top row).
The problem is to change their positions to those shown at the bottom of the illustration in the shortest possible number of moves.
A move consists of placing the tips of the first and second fingers on any two touching coins, always of the different sizes, then sliding the pair to another spot along the imaginary line shown in the illustration. The two coins in the pair must touch at all times. The coin at left in the pair must remain at left; the coin at right must remain at right. Gaps in the chain are allowed at the end of any move except the final one. After the last move the coins need not necessarily be at the same spot on the imaginary line that they occupied at the start.
Coin Butterfly
by Peter Grabarchuk
Two equilateral triangles are created with the help of five identical coins. Slide only two coins so that the equilateral triangles are now both of different size.
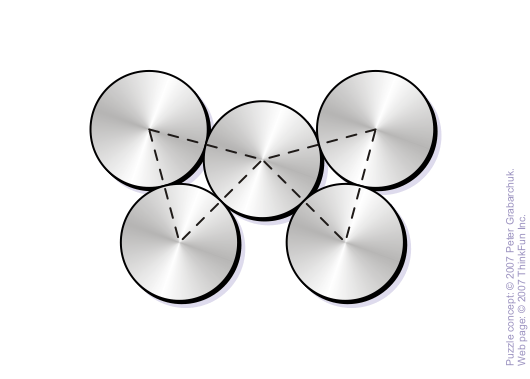
Five identical coins are arranged into the shape shown in the illustration. As it can be seen centers of the coins lie in the vertices of two identical equilateral triangles shown with the dotted lines.
Make only two single-coin moves and create two different equilateral triangles instead of these identical ones. A single-coin move consists of sliding a coin to new position where it must touch at least two other coins.

Four Stacks
after Martin Gardner
Tumping over two coins every time rearrange a row of eight coins into four stacks of two coins each. It can be done in four jumps – just keep jumping.
Place eight coins in a row as shown in the illustration. The object is to make from all the coins four stacks of two coins each and it should be done in four moves only.
Every move consists of jumping of a coin over any two coins (no matter lying flat or in a stack) in one direction, and stopping on the top of the next coin.

The Jumping Coins
What can prevent you from moving the coins forward to the aim of the puzzle? Ironically, but it’s the rule of “forward-move-only” that can do it.
This puzzle was described by Edouard Lucas at the end of the 19th century.
Place three quarters and three pennies in a line of seven cells as shown in the left illustration – quarters on the left, and pennies on the right. The middle cell is empty.
Now interchange two groups of coins moving quarters to the right and pennies to the left. The middle cell has to be empty when you finish.
Coins are moved just in a forward direction. This means you have to move quarters to the right and pennies to the left only. A move consists of moving a coin on the adjacent vacant cell, or jumping over an adjacent coin on the vacant cell immediately behind it.
